Арифметический треугольник – это треугольник Паскаля или треугольная числовая таблица для составления биномиальных коэффициентов (формула бинома Ньютона). По бокам арифметического треугольника стоят единицы, внутри — суммы двух верхних чисел.
В (n+1)-й строке арифметического треугольника — биномиальные коэффициенты для разложения бинома (а+b)n. Этот арифметический треугольника был приведён в 1665г. в книге Блез Паскаля «Трактат об арифметическом треугольнике». Треугольник Паскаля часто выписывают в виде равнобедренного треугольника, в котором на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух расположенных над ним чисел.
Итак, что такое арифметическая прогрессия высшего порядка? Разберемся по порядку.
Арифметическая прогрессия — это последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего путем добавлением к нему постоянного числа (шага, или разности прогрессии). Это арифметическая прогрессия первого порядка.
Аналогично можно ввести более высокие прогрессии — третьего порядка — её разности образуют прогрессию второго порядка, четвёртого порядка — её разности образуют прогрессию третьего порядка, и так далее любую другую прогрессию.
Самым знаменитым примером прогрессий высших порядков являются последовательности степеней. Например,
1 2 3 4 5 — прогрессия первого порядка
1 4 9 16 25 — прогрессия второго порядка
1 8 27 64 125 — прогрессия третьего порядка
А теперь рассмотрим пример получения арифметической прогрессии высших порядков. Для примера возьмём прогрессию третьего порядка: 1 5 12 24 …
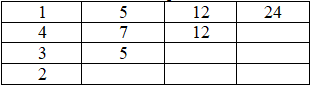
Как найти её последующие члены? В первую очередь, нужно знать порядок прогрессии, то есть то, что она третьего порядка. На основе данных нам четырёх членов, мы можем составить последовательности разностей. Составим следующую схему:
Теперь на основе этой прогрессии мы можем продолжить вторую строку первой таблицы вправо:
Мы отталкивались от последней строки, а в последней строке у
нас было только одно число — 2. Значит, нам нужно знать первый член последней
строки.
В предпоследней строке мы просто прибавляли везде 2, но с
самого начала у нас было 3. Значит, мы
должны знать также первый член предпоследней строки. Далее нам нужно знать
первые члены всех остальных строк. Таким образом, чтобы строить таблицу, нам
достаточно знать всего 4 числа.
Также необходимо понимать, что n-й член в строке равен сумме первого члена в этой строке со всеми членами строки ниже вплоть до (n-1)-го члена. Например, 24 = 1 + 4+7+12
А мы знаем формулу суммы прогрессии первого порядка.
Значит, n-й член прогрессии второго порядка равен
Для удобства, будем нумеровать члены с нуля:
Исследовав прогрессии высших порядков в треугольнике Паскаля, можно составить алгоритм их получения. Рассмотрим его на примере получения арифметической прогрессии 8-го порядка.
1. Для начала нам нужно выписать в треугольнике Паскаля прогрессии более низших порядков:
Причем заметим, что 45=
1+8+36 предыдущей последовательности…
Причем 165= 1+8+36+120
предыдущей последовательности…
Таким образом, чтобы найти число, стоящее в арифметической прогрессии начиная со второго порядка можно воспользоваться алгоритмом: Чтобы получить число, стоящее на n-ом месте в прогрессии, нужно сложить (n-1)-й член последовательности и n-ый член из прогрессии предыдущего порядка.
Таким образом, в треугольнике Паскаля можно обнаружить следующую арифметическую прогрессию 8-го порядка: 1; 9; 45; 165; 495; 1287; 3003; 6435; 12870…
Вывод: на картинке ниже
по диагоналям справа-налево и одновременно сверху-вниз цветом выделены
арифметические прогрессии: Нулевого порядка. Первого порядка. Второго порядка.
Третьего порядка. Четвертого порядка и так далее.
В математике много интересных загадок, фактов, в том числе и в треугольнике Паскаля. А некоторые даже неизвестны до сих пор….